Back in the first investigation we looked at figure eights, also known as lemniscates. We decided that the equation for a lemniscate with foci at (-a, 0) and (a, 0) was . Now we are going to revisit the lemniscate but we are going to look at it using a different kind of mathematical tool. In the last investigation we learned how to plot using parametric equations instead of the traditional rectangular coordinates. Now we are going to learn to plot another way, using polar coordinates. Once we understand what polar coordinates are we can go back and look at how the figure eight can be explored using our new knowledge.

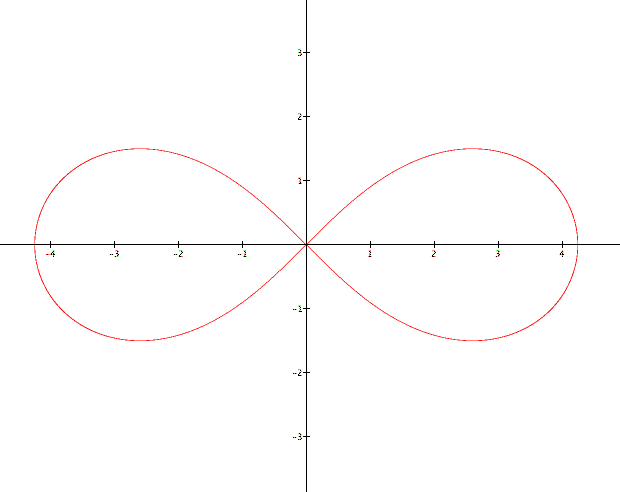
In the last investigation we learned how we can represent graphs using parametric equations. The point of being able to use parametric equations was to be able to answer questions more easily than if we were using rectangular coordinates. Polar coordinates play a similar role. They allow us to work with equations and plot them more easily than if we tried to use rectangular coordinates. The way we think of a point on a graph with rectangular coordinates is (x, y) where x is the horizontal distance from the origin to the point and y is the verticle distance from the origin to the point.

Now we are going to think of the point in a different way. Imagine drawing a line segment from the origin to our point of interest. The two things we are going to look at is the length that line segment, which we denote by r, and the angle that segment makes with the positive half of the x-axis.

It should make since that because we are representing the same point two different ways that there should be a relationship between the rectangular coordinates and the polar coordinates. Indeed, there is. Let's combine the important aspects of the point for the two coordinate systems onto one picture.

We are going to take the verticle line segment, y, and shift it to the right so that we are working with a triangle.

Now let's use our definitions of sine and cosine to find a relationship between the variable in this picture.

Solve for x and y to see how polar coordinates and rectangular coordinates are related.

As you can see, we can go back and forth between rectangular coordinates and polar coordinates if need to. Or we can just choose which coordinate system is most beneficial to us during any given problem.

Let's return to the problem of the lemniscate and look at it from the point of view of polar coordinates. In rectangular coordinates the equation was

Using what we just found we can convert this to polar coordinates using substitution.

I ask you, which looks nicer to work with or ?

Assume for the moment that a=1. Let's plot a few points so that you can see how to work with polar coordinates. We are going to plot for various as the table beneath dictates.

	0	/6	/4	/3	/2	2/3	3/4	5/6		7/6	5/4	4/3	3/2	5/3	7/4	11/6	2
2	0	/3	/2	2/3		4/3	3/2	5/3	2	7/3	5/2	8/3	3	10/3	7/2	11/3	4
cos(2)	1	1/2	0	-1/2	-1	-1/2	0	1/2	1	1/2	0	-1/2	-1	-1/2	0	1/2	1
2cos(2)	2	1	0	-1	-2	-1	0	1	2	1	0	-1	-2	-1	0	1	2
r		1	0	DNE	DNE	DNE	0	1		1	0	DNE	DNE	DNE	0	1

Since the origin was plotted several different times its coordinates for left out so that the picture did not become too cluttered. You can imagine connecting these points and getting the lemniscate. If you can't see that then try adding more points to the graph and plotting those. Another small change in our picture is that is measured in radians in our chart and in degrees in our picture. If you do not feel comfortable with that then translate our chart on paper. This is good practice and you should be able to go from radians to degrees and back with little effort.

Now that we have the equation for the lemniscate in polar coordinates let's explore what happens when we vary parts of this

equation.

Since the range for is -1 to 1 it would make sense that changing the value for a would change the range for , which is from 0 to (why is the lower limit 0 instead of -?). That means the lemniscate will be streched out when a is changed. The picture below confirms this. It is a lemniscate that has the form when a=0, 1, 2 and 3.

Now let's think of the general form of a lemniscate as being . What happens when we change b? This is harder to predict so let's just see what kind of pictures we get when b=-2, 0, 2.

It appears to be spinning the graph. That happens because at any given we are getting different radii lengths. Still confused? Rewrite our equation for the lemniscate by using additive angle formulas.

Can you see that if our parent equation was

then when we add b on the inside we are essentially taking our old and multiplying it by the constant and then adding to that the new new value for . Now knowing what you do about values for the trigonimetric functions at various values see if you can understand why we get the pictures above. Given a value for b, can you predict how the lemniscate will look? Notice that if b equals 2 or any integer multiple of 2 then sin(b)=0 and cos(b)=1. Then since

we get that

In other words, adding b inside makes no difference to the graph when b is a multiple integer of 2.

There are so many things that can explored with this problem that there just isn't enough time. What happens if cos(2) is replaced with sin(2) or tan(2)? What about if we change it to ? What happens if 2 becomes 3 or -5? What if we add values to the end of our polar coordinate equation so that the general form looks like or ? Which c values result in the figure eight and which ones cause our graph to fall apart? How can these be predict? Why are they behaving in such a way? So much math, so little time.... Have fun exploring.

Return